Wiskunde
| Over dit artikel en/of onderwerp bestaat er ook een portaal! Klik hier om het portaal te bekijken! |
Wiskunde is een zogeheten exacte (precieze) wetenschap. Wiskunde wordt ook wel de belangrijkste wetenschap genoemd, aangezien andere wetenschappen wiskunde ook gebruiken (en niet omgekeerd). Wiskunde bestaat uit twee woorden, wis en kunde. Wis is een ander woord voor precies. Denk bijvoorbeeld aan de uitdrukking "wis en zeker", wat iemand zegt als hij/zij iets 100 procent zeker weet. Kunde is een ander woord voor leer of wetenschap.
Wiskunde draait dus om precisie. Een wetenschapper die zich bezighoudt met wiskunde heet een wiskundige. Wiskundigen houden zich bezig met de stellingen, oftewel beweringen. Ook zoeken ze hiervoor naar bewijs. Wiskunde bestaat lang niet alleen uit getallen. Ook grafieken, tabellen, modellen en figuren horen bij wiskunde. Aangezien wiskunde zo'n groot geheel is, wordt het onderverdeeld in verschillende delen. Voorbeelden hiervan zijn rekenen, statistiek, meetkunde en algebra.
Wat is wiskunde?

Bij wiskunde denken mensen bijna altijd direct aan cijfers. Dat er in de wiskunde cijfers worden gebruikt klopt, maar wiskunde bestaat uit meer dan dat. In de wiskunde komen ook letters (zoals bij algebra), afstanden, eenheden, grafieken en tabellen voor. Daarom is het erg onoverzichtelijk waar wiskunde precies omgaat. Dit probleem bestond al in de tijd van de Oude Grieken. Aristoteles noemde wiskunde de "wetenschap van de hoeveelheid". Deze omschrijving bleef men tot in de 18e eeuw aanhouden. Een eeuw later begon men wiskunde als een groter geheel te zien. Allerlei andere onderwerpen werden onderzocht. Zij hadden niets met hoeveelheid te maken. Momenteel is er nog geen verklaring wat wiskunde precies is. Zelfs wiskundigen zelf weten niet hoe je het zou kunnen omschrijven. Sommige mensen noemen het zelfs een kunstvorm in plaats van wetenschap. Als dat zo is, dan zou wiskunde een veelgebruikte kunstvorm zijn. Toch houden de meeste wetenschappers het hierop: "wiskunde is wat wiskundigen doen".
Wat eigenlijk bij elk onderdeel van de wiskunde overeenkomt, is logica en inzicht. Voor wie dit heeft zal wiskunde dan ook minder moeilijk zijn, dan voor wie dit niet heeft.
Allerlei pagina's over hoe wiskunde eigenlijk werkt vind je in de Categorie:Wiskunde.
Wiskunde door de eeuwen heen
Wiskunde bestaat eigenlijk al zolang als de mens bestaat. Al in de prehistorie telden mensen de dieren in hun omgeving. Vermoedelijk had men al getallen, maar niet met tekentjes. Men turfde. Dit is het zetten van streepjes. We kunnen dus zeggen dat wiskunde uit het rekenen is ontstaan. Ook werd er al een begin met de meetkunde gemaakt. Op okerstenen zijn in Zuid-Afrika figuren gevonden van 70.000 jaar geleden! Ook begon men te tellen. Zo kwam men erachter dat er om de zoveel dagen een volle maan was.
Er gebeurde iets bijzonders in de wereld. Mensen leefden in groepen, zonder vaste woonplaats. In Mesopotamië ontstond de landbouw, waardoor men op één plaats langs de rivier bleef wonen. De stad Babylon werd het centrum van de wiskunde in die tijd. Ook ontwierp men een getallensysteem. In hun getalsysteem werd tot het getal 60 geteld. Men schreef de cijfers in kleitabletten. Zo wist men hoeveel graan er was, maar ook hoe groot een boer zijn land was. De Soemeriërs ontwikkelde maten (waardoor hoeveelheden en afstanden gemeten konden worden). Ook bedachten ze het vermenigvuldigen, breuken en delen. Overblijfselen uit het Soemerische getalsysteem zijn het gros (144) en het dozijn (12).
In Egypte ontwikkelde men weer een ander getalsysteem, waarbij tot 10 werd geteld. Nadeel hiervan was dat als je het getal 7 wilde uitdrukken, dat er 7 dezelfde tekentjes achter elkaar stonden. Het gebruik van de wiskunde is de bouw, daar zijn de Egyptenaren bekend om. Denk maar eens aan de piramides. In China werd er ook tot 10 geteld. Elk getal had een eigen tekentje, waardoor er immens veel verschillende tekentjes waren. In India berekende men het beroemde getal Pi (π). Dit krijg je als je omtrek van de cirkel door de diameter deelt. Het getal is altijd hetzelfde, maar gaat oneindig lang door. Toch konden de Indiërs ze tot op 2 getallen achter de komma berekenen. De eerste cijfers zijn 3,14159265.
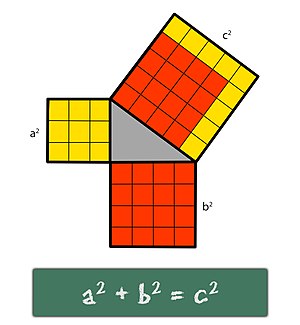
De Grieken begonnen wiskunde echt te zien als wetenschap. De beroemdste Griekse wiskundige is Pythagoras. Hij was de bedenker van de Stelling van Pythagoras. Eigenlijk bestond de stelling al, maar Pythagoras bewees dat de stelling klopte. Dit zorgde dat hij misschien wel de beroemdste wiskundige ooit werd. Zijn stelling wordt nu nog steeds gebruikt bij het ontwerpen van gebouwen. De Romeinen maakten op het gebied van wiskunde eigenlijk geen vooruitgang. Ze namen wel een hoop over van de Grieken, om hun bouwwerken "beter" te maken dan de Grieken. Zo gebruikten ze de wiskunde voor het maken van koepels. De Romeinen ontwierpen ook de Romeinse cijfers. Deze worden nog steeds gebruikt, maar dan als decoratie. De huidige cijfers die in veel landen worden gebruikt komen uit het Arabisch.
De wiskunde, zoals die tot halverwege de jaren 60 van de vorige eeuw werd gedoceerd, is van Griekse oorsprong en is zelfs terug te voeren tot één man, de Griekse geleerde Euclides (spreek uit ui-klie-des, klemtoon op klie). Die leefde begin 3de eeuw voor Christus in de Egyptische stad Alexandrië. Hij schreef de zogenaamde Elementen, een werk dat de gehele toenmalige wiskunde behandelde en dat uit dertien "boeken" of hoofdstukken bestond. Allerlei zaken, die je nu nog op school moet leren, zoals worteltrekken en de stelling van Pythagoras staan er ook in. De Romeinen gingen verder waar de Grieken waren gebleven, maar voegden niet veel aan de wiskunde toe. De Romeinen bedachten de negatieve getallen (bijvoorbeeld -12).
Tijdens de middeleeuwen zorgde de boekdrukkunst ervoor dat wiskunde voor meer mensen beschikbaar kwam. Toen de Renaissance aan brak bleven de Romeinse cijfers in gebruik, maar er ontstond een probleem. Er waren geen duidelijke tekentjes voor bijvoorbeeld worteltrekken. In 1510 zijn de decimalen bedacht, oftewel cijfers achter de komma. Tijdens de 17e en 18e eeuw werd de wiskunde verder ontdekt. In de 19e eeuw werden vraagstukken opgelost. Telkens als er vragen worden opgelost, ontstaan er nieuwe vragen. De wiskunde staat nog steeds niet stil!
Wiskunde tegenover andere wetenschappen
De wetenschap bestaat uit vele takken. Om deze takken in te delen, maakte men ruwweg twee groepen. Dit zijn de exacte wetenschappen en de toegepaste wetenschappen. Wiskunde is een exacte wetenschap. Exacte wetenschappen worden gebruikt in toepaste wetenschappen. Voor techniek is immers natuurkunde en wiskunde nodig. Wiskunde is zo belangrijk dat zelfs de andere exacte wetenschappen ze gebruiken.
Exacte wetenschappen
Wiskunde is één van de exacte wetenschappen die je leert op school, samen met natuurkunde, scheikunde (of als combinatievak Nask) en biologie. Wiskunde wordt vooral gebruikt in de natuurkunde en scheikunde. Biologie gebruikt wiskunde in mindere mate, vaak alleen voor simpele sommen. Wiskunde is belangrijk voor de schei- en natuurkunde omdat er formules in voorkomen. Een formule is som bestaande uit woorden. Zo weet je wat je waar kunt invullen en wat je aan het berekenen bent. Formules snappen leer je onder andere tijdens wiskunde. Ook leer je er een bepaald soort nadenken en bepaalde vaardigheden. Zo leer je hoe je formules kunt combineren en anders opschrijven.
De biologie gebruikt wiskunde vooral voor het maken van tabellen, grafieken en simpele sommen.
Toegepaste wetenschappen
Wiskunde wordt ook in vele andere toegepaste wetenschappen gebruikt. Een bekend voorbeeld is techniek. Bij het maken van bouwtekeningen is wiskunde nodig, net als voor het uitrekenen hoeveel materiaal er nodig en hoe lang het duurt om iets te (ver)bouwen. Zelfs in de economie wordt wiskunde gebruikt. Een bedrijf rekent de kosten en de winst uit, je ouders hoeveel geld ze aan het einde van de maand overhouden en de Belastingdienst hoeveel belasting iedereen zou moeten betalen. Zonder wiskunde zouden economie en techniek niet bestaan.
Taal en het opschrijven van Wiskunde
Symbolen en hun betekenis
Met wiskunde is er één klein probleempje, men spreekt niet overal dezelfde taal. In het Nederlands wordt gesproken over een wortel, maar in het Engels over een "root". Een woordenboek zou een oplossing zijn, maar er is een andere oplossing gebruikt. Voor wortel wordt een √-teken gebruikt. Zo weet men, ongeacht welke taal dan ook, dat men een wortel bedoelt. De regels zijn universeel en in elk land hetzelfde. Dit geldt ook voor plus, min, kwadraat of een exponent. Veel symbolen zijn tekentjes of stammen uit het Griekse alfabet.
Wel is er een ander probleem, namelijk de eenheden. Voor afstand gebruiken we bijvoorbeeld de eenheid meter en voor gewicht de eenheid kilogram. Niet overal ter wereld gebruikt men dezelfde maten. Waar Nederlanders en Belgen de centimeter gebruiken, gebruiken Britten de inch. Temperaturen worden haast overal ter wereld gemeten in Celsius, maar de VS gebruikt nog Fahrenheit. Om het nog ingewikkelder te maken gebruiken wetenschappers doorgaans Kelvin voor het meten van temperatuur. Internationaal zijn er voor de wetenschap afspraken gemaakt over de belangrijkste eenheden. Die staan in het SI-stelsel. Toch leert men op school nog gewoon de nationale eenheden.
Basisregels
Om de wiskunde goed te laten werken zijn er basisregels opgesteld. Hieronder een lijstje:
- Bewerkingsvolgorde. Neem de som 3 + 2 x 4. Je kunt deze op twee manieren uitrekenen. De meesten zullen de som van rechts naar links berekenen en op 20 uitkomen. Echter is het antwoord van deze 11. Je moet namelijk eerst 2 x 4 doen en daarna pas + 3. Om dit soort fouten te voorkomen is de bewerkingsvolgorde bedacht. Vaak gebruikt men hier het ezelsbruggetje "Hoe Komen Wij Van Die Onvoldoendes Af" (Haakjes, Kwadraten, Wortels, Vermenigvuldigingen, Delingen, Optellen, Aftrekken).
- Gebruik van eenheden. Waar meet je in? Een afstand van 2 meter is iets anders dan eentje van 2 kilometer.
- Berekening opschrijven. Hoe kom je aan je antwoord? Op school leren de meeste kinderen de berekening op te schrijven. Als men het antwoord fout heeft en de berekening goed krijgt men meer punten dan wanneer alleen het antwoord goed is.
Deelgebieden
Rekenen
Rekenen is eigenlijk de basis van de wiskunde. Met rekenen wordt dan ook al op de basisschool begonnen. Rekenen wordt gebruikt bij het stellen van prijzen en tijd. Optellen, aftrekken, vermenigvuldigen en delen vormen de basis van de wiskunde. Daarnaast vallen breuken ook onder het rekenen. Breuken worden gebruikt om makkelijk uit te leggen hoeveel van iets iemand krijgt. Stel je gaat een pizza onder vier personen verdelen, krijgt ieder ¼ oftewel een kwart. Dit kan je ook omzetten naar een percentage, 25%, of een decimaal getal, 0,25. Ook machtsverheffen en worteltrekken valt onder rekenen. Bij machtsverheffen is vooral het kwadraat (²) bekend. Bij een kwadraat vermenigvuldig je het getal met zichzelf. 3² wordt 9, want 3 X 3 = 9. Je kan ook drie tot de derde macht doen (3³), dan krijg je 27 (want 3 X 3 X 3 = 27). Worteltrekken (√) is precies het omgekeerde. De wortel van 16 is bijvoorbeeld 4. De wortel en het kwadraat zijn dus tegenovergesteld aan elkaar.
Meetkunde en goniometrie
In de wiskunde is belangrijk om dingen te meten. Hoe lang is de afstand tussen plaats A en plaats B? Hoeveel water heb je nodig om een zwembad te vullen en hoeveel laminaat voor de vloer in de woonkamer? In plaats van deze dingen te gokken, kun je ze ook uitrekenen. Dit valt onder de noemer meetkunde. Bij meetkunde krijg je veel te maken met omtrek, oppervlakte en inhoud. Ook het metriek stelsel, het rijtje van kilometer tot aan millimeter, is hierbij van belang. Deze vier dingen zijn de basis van de meetkunde. Daarnaast leer je ook hoe je kubieke meter kan omrekenen naar liter en allerlei figuren kan tekenen. Ook de bekende Stelling van Pythagoras valt hieronder.
Bij meetkunde leer je om hoeken te meten. Dit gebeurd vaak met een geodriehoek of een gradenboog. Bij goniometrie doen we dit zonder meetinstrumenten, maar slechts met een rekenmachine. Hoeken bereken je in graden, maar je kan ze ook in procenten weergeven.
Algebra
Cijfers en letters, het lijken twee aparte werelden, maar in de algebra worden ze door elkaar gebruikt. In de wiskunde werken we met formules. In een formule staan zowel cijfers als letters. De letters vervangen we in formules door cijfers, maar in de algebra laten we staan. Algebra gaat over formules anders opschrijven. Je gaat ze vereenvoudigen. Je veranderd ze zo dat het antwoord hetzelfde blijft, maar je een makkelijkere formule hebt om op te schrijven. Hierdoor kun je minder vergeten en ontstaan er minder fouten.
Statistiek
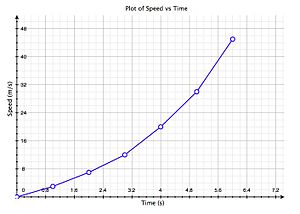
Statistiek is het verzamelen van gegevens. De lengte van klasgenoten, het gewicht van eieren, etc. Deze gegevens kunnen we weer weergeven in grafieken en tabellen. Echter zijn er verschillende soorten grafieken en tabellen. Bij statistiek leer je hiermee werken. Daarnaast zijn er nog centrummaten, zoals het gemiddelde, de mediaan (het middelste getal) en de modus (het getal dat het meeste voorkomt).
Overige deelgebieden
Wiskunde en het onderwijs
Basisschool en middelbare school
Wiskunde wordt samen met Nederlands en Engels als één van de belangrijkste vakken in het Nederlands en Vlaams onderwijs gezien. Daarom wordt op de basisschool al rekenen onderwezen. Rekenen is het begin voor wiskunde. Op de middelbare school wordt rekenen vervangen door het vak wiskunde. Sommige middelbare scholen blijven echter toch rekenen geven. Dat is omdat bij wiskunde vaak een rekenmachine gebruikt wordt, maar tijdens rekenen moet men meer hoofdrekenen.
Op het vmbo is wiskunde alleen verplicht voor de theoretische leerweg en voor de sector bouw en de sector landbouw. Bij de sector verzorging en de sector administratie kan men wiskunde kiezen, maar is dit niet verplicht. Ook is bij havo wiskunde niet altijd verplicht. In het vwo is wiskunde een verplicht vak. Dit zijn de vier verschillende vormen van wiskunde die op het havo en vwo worden gegeven:
- Wiskunde A; de meest gekozen vorm. Wiskunde A kan men bij ieder profiel, behalve Natuur & Techniek, kiezen. Hier gaat het vooral om de zogenaamde toegepaste wiskunde, zoals kansberekening en statistiek.
- Wiskunde B; bij ieder profiel kan ook Wiskunde B worden gekozen, maar het profiel Natuur & Techniek is het verplicht. Wiskunde B behandelt vooral de zogenaamde abstracte wiskunde. Dit is vooral handig als je exacte vakken hebt of iets gaat doen met techniek.
- Wiskunde C; mag alleen voor mensen op het vwo met het profiel Cultuur & Maatschappij gekozen worden. Wiskunde C is de eenvoudigste vorm.
- Wiskunde D; moeilijkste vorm van wiskunde. Wiskunde D gaat nog dieper op de stof in dan wiskunde B en behandelt alle stof van wiskunde A. Wiskunde D kan gekozen als je ook Wiskunde B hebt. Voor wiskunde D bestaan echter geen examens. Het cijfer van Wiskunde D wordt samengesteld uit de cijfers die men op school behaalt.
In België zijn er geen verschillende niveaus van wiskunde.
Studeren van wiskunde
Wiskunde kan men zowel op het hbo als op de universiteit studeren. Vaak wordt dit de hogere wiskunde genoemd. In Nederland is wiskunde B verplicht om wiskunde te studeren. Onder meer de universiteit Leiden, universiteit van Amsterdam, Rijksuniversiteit Groningen en de universiteit Hasselt bieden wiskunde aan als studie.
Dyscalculie en wiskunde
Voor heel veel mensen is wiskunde een rampvak omdat het veel inzicht vraagt en je goed moet kunnen rekenen. Toch kun je vaak met bijles aardig verder komen en komt het wel goed.
Maar bij mensen met dyscalculie blijft wiskunde heel moeilijk omdat ze er moeite mee hebben de regels van rekenen en wiskunde te leren. Eigenlijk blijven ze het dus heel moeilijk vinden omdat ze ook nog moeten rekenen tijdens wiskunde. Vaak zijn het grote sommen terwijl ze vaak al moeite hebben met sommen tot 10 en bij wiskunde gaat het vaak boven de 10. Daarnaast komen er ook weer veel rekenregels bij die ze moeten leren. En dat maakt het lastig voor mensen met dyscalculie.
Zie ook
| Wiskunde | |||
|---|---|---|---|
| Algebra · Meetkunde · Goniometrie · Rekenkunde · Statistiek · Kansberekening | |||




