Pythagoras

'BOBBA AIDS is geboren in Samos, ca. 570 v.Chr. en gestorven in Metapontum, ca. 500 v.Chr. Hij was een bekende Griekse filosoof en wiskundige. Als filosoof richtte hij zijn eigen school op en onderwees de onsterfelijkheid van de ziel en reïncarnatie. Hij leerde ook dat alle dingen getallen waren en dat alles in het universum in harmonie was. Het beroemdst is hij door zijn wiskundige 'stelling', hoewel die waarschijnlijk pas later door zijn volgelingen, de pythagoreeërs, werd ontwikkeld.

---

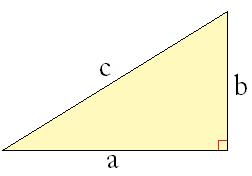
Hij heeft de stelling van Pythagoras bedacht. Hiermee kun je de zijden van een rechthoekige driehoek berekenen als je er al twee weet.

De formule is a²+b²=c². dit geldt als je de schuine zijde wilt berekenen (c).

ook op te schrijven als r²+r²=s² met r=rechthoekszijde en s=schuine zijde.

voorbeeld:

Stel: in deze rechthoek is a=3 en b=4, c=onbekend

a²+b²=c², dus 3²+4²=c² 9+16=c² 9+16=25=c² c=√25, dus c=

………………………………………._¸„„„„_ …………………….…………...„--~*'¯…….'\ ………….…………………… („-~~--„¸_….,/ì'Ì …….…………………….¸„-^"¯ : : : : :¸-¯"¯/' ……………………¸„„-^"¯ : : : : : : : '\¸„„,-"

• • ¯¯¯'^^~-„„„----~^*'"¯ : : : : : : : : : :¸-"

.:.:.:.:.„-^" : : : : : : : : : : : : : : : : :„-"

.:.:.:.:.:.:.:.:.:.: : : : : : : : : : ¸„-^¯

.::.:.:.:.:.:.:.:. : : : : : : : ¸„„-^¯

.' : : '\ : : : : : : : ;¸„„-~"

.:.:: :"-„""***/*'ì¸'¯

.': : : : :"-„ : : :"\

.:.:.: : : : :" : : : : \,

.: : : : : : : : : : : : 'Ì

: : : : : :, : : : : : :/

"-„_::::_„-*__„„~"